Load transfer

Load transfer describes the change in load of tires on a vehicle during acceleration. Load transfer is often confused or referred to as weight transfer. This leads to unclear language usage. Weight transfer describes the physical movement of a vehicles center of mass through suspension compliance and fluid sloshing.

Load Transfer vs Weight Transfer

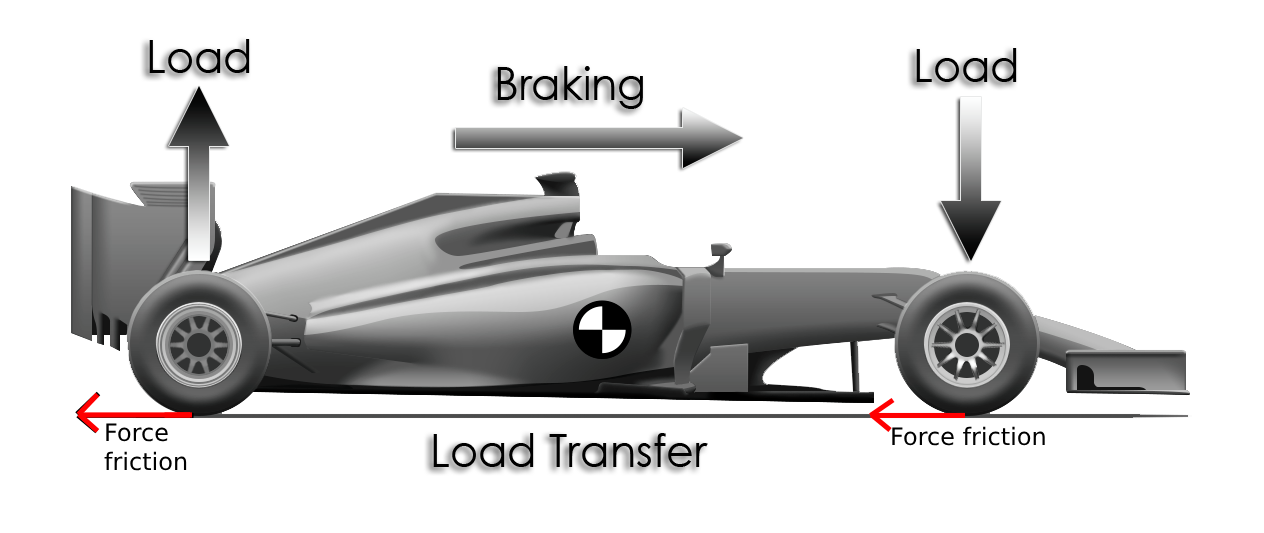
Load transfer under braking on a completely rigid vehicle

Load transfer is a change in load borne by tires during any acceleration. The tires of a vehicle are what provide the force. However, the contact patch of the tires is not in the same location as the center of mass of a vehicle. Thus, you must treat the vehicle as a real system rather than a point particle one. This difference in location of force and center of mass subsequently causes a roll moment (think of it as a torque kinda), loading a set of tires more than the other. For example, when a completely rigid vehicle brakes, it is deaccelerating by the force of the tires' contact patch, and because the vehicle's Center of Mass is vertically higher up than the tires' contact patches, the load of the rear tires will decrease, and the load of the fronts will increase. Load transfer also occurs laterally when turning due to centripetal force (which is acceleration).

Weight transfer is the change in the center of mass of a vehicle through suspension compliance and cargo/fluid movement. For example, when a vehicle accelerates forward, fluids and unsecured cargo will travel rearwards relative to the vehicle, thus shifting the center of mass rearward.

Load transfer matters significantly more than weight transfer. This is because load transfer determines the traction a given tire has and the traction the car as a whole has much more significantly than weight transfer. Additionally, your FSAE car should not have unsecured cargo. Any weight transfer that occurs on our car will be due to fluids and suspension compliance (which is relatively stiff anyway) and thus the center of mass barely moves.

To emphasize the minuscule effect of weight transfer compared to load transfer, here is an example I copied from Wikipedia: "For instance in a 0.9g turn, a car with a track of 1650 mm and a CoM height of 550 mm will see a load transfer of 30% of the vehicle weight, that is the outer wheels will see 60% more load than before, and the inners 60% less. Total available grip will drop by around 6% as a result of this load transfer. At the same time, the CoM of the vehicle will typically move laterally and vertically, relative to the contact patch by no more than 30 mm, leading to a weight transfer of less than 2%, and a corresponding reduction in grip of 0.01%."

Calculate it

Longitudinal

The change in load of the front wheels (longitudinal) can be determined using the following:

$\mathrm{\Delta }Loa{d}_f{}_r{}_o{}_n{}_t=-a\frac{h}{b}m$

Where delta Load front is the change in front load, a is longitudinal acceleration, h is the height of the center of mass, b is the wheelbase length, and m is the total mass of the vehicle. Change in rear load can be found by ignoring the negative. If the center of mass is not in the middle of the car laterally, a coefficient Cx can be added to find the load change of each wheel.

$R=\frac{e}{\frac{t}{2}}$

Where R is the offset ratio, e is the distance the center of mass is from the center line and t is the front trackwidth. R must be calculated for both the front and rear. To calculate rear R, use rear trackwidth rather than front trackwidth for t.

$Cx=\frac{1}{2}\times (1\pm R)$

Cx is the load adjustment coefficient, R is offset ratio. Cx must be calculated for each wheel. If the Cx you are generating is for a wheel laterally closer to the center of mass, add R to 1, otherwise subtract R from 1.

Multiply each front wheel's Cx by the change in front load to get the change in load of each front wheel. Multiply each rear wheel's Cx by the change in rear load to get the change in load of each rear wheel.

Laterally

The total change in tire load laterally across the whole car when cornering on a can be determined using:

$LLT=\frac{Ay\times h\times m}{t}$

• LLT is total lateral load transfer occurring across the car
• Ay is lateral acceleration, h is the height of the center of mass
• m is the overall vehicle mass,
• t is the average trackwidth.

For example, a car making a right turn at 0.9g's, with a ride height of 0.3m, and a trackwidth of 0.75m will have an LLT of 0.36, or 36%. This means the lateral load transfer occurring across this car is 36% of the total mass of the vehicle. On a car with equal split mass this mean the left (outside) wheels would have 86% of the load. If the LLT is above 50%, this means the inside wheels have left the ground.

Note roll center and roll stiffness are not present in this equation. The total magnitude of lateral load transfer cannot be changed by modifying the suspension. However, the distribution of lateral load transfer front vs rear can be changed through suspension modification. This will change the oversteer vs understeer bias the car possesses.

Lateral Load transfer Distribution

To find the total lateral load transfer on a given axle, link (inelastic) load transfer, roll stiffness (elastic) load transfer, and unsprung load transfer must be found and summed. However, unsprung load transfer is negligible.

Remember, load transfer across both axles (aka the whole vehicle) cannot be changed with roll stiffness nor moving the roll center. However, the distribution of total lateral load (LLT) can be changed between the front and rear axles through changes to the roll center height and roll stiffness.

These equations assume steady state cornering, does not take into account movement of the roll center, assume the tires have infinite stiffness, assume suspended CoM and weight is equivalent to chassis CoM and weight, and prolly other things I'm forgetting.

Link Load Transfer

Link load transfer is a result of the moment arm created by the lateral force of the tire's contact patches acting upon the chassis through the suspension arms. The effective point of application is the roll center. The change in tire vertical load for an axle due to link load transfer can be found using:

$\mathrm{\Delta }W=\frac{m\times Hrc\times }{t}\times a$

• delta W is the change in tire vertical load due to link load transfer
• m is the mass supported by the axle
• Hrc is the height of the roll center
• a is the lateral acceleration.

Notice, delta W is the change in tire vertical load only for one axle where LLT is the total change across both axles.

Roll Stiffness Load Transfer

Roll stiffness (elastic) load transfer is the change in vertical tire load generated by the moment arm between the center of mass and the roll center. The roll moment must be counter-acted by roll stiffness during steady state cornering, thus roll stiffness load transfer is proportional to the roll stiffness of the suspension. To put simply, elastic load transfer for a given axle is:

$\mathrm{\Delta }E=\frac{K_{\theta }\times \theta }{t}$

• deltaE is the change in vertical tire load due to elastic load transfer
• K theta is the total roll stiffness
• theta is the roll angle of the suspended mass
• t is the tract width of the given axle

Although that equation looks quite simple, it is essentially useless for understanding. Note on the next equations, f indicates front and r indicates rear. The expanded version for the front axle looks like the following:

$\mathrm{\Delta }{E}_f=\frac{K_{\theta }{}_{,}{}_f}{K_{\theta }{}_{,}{}_f+K_{\theta }{}_{,}{}_r}[\frac{m_f(Hcg-Hr{c}_f)+m_r(Hcg-Hr{c}_r)}{t_f}]a$

• deltaE is the change in vertical tire load due to elastic load transfer
• K theta is the total roll stiffness
• m is the mass supported by the axle
• Hcg is the height of the center of gravity
• Hrc is the height of the roll center
• t is the tract width
• a is the lateral acceleration

In the expanded equation it can be seen that despite the calculations being for the front axle, the rear mass, rear roll stiffness, and rear roll center height are components. This is why changing the distribution of the total lateral load transfer does not change its total value.

For the rear axle the equation is:

$\mathrm{\Delta }{E}_r=\frac{K_{\theta }{}_{,}{}_r}{K_{\theta }{}_{,}{}_f+K_{\theta }{}_{,}{}_r}[\frac{m_f(Hcg-Hr{c}_f)+m_r(Hcg-Hr{c}_r}{t_r}]a$

"Total" load transfer for ONE axle

Total load transfer of a single axle is the sum of the axle's link load transfer, and it's roll stiffness (elastic) roll transfer.

Taking the derivative of the change in tire vertical load with respect to lateral acceleration is the lateral load transfer sensitivity. This is the incremental change in vertical tire load per unit lateral acceleration. For example, this is the formula for the lateral load transfer sensitivity for the front axle:

$\frac{d\mathrm{\Delta }TOTA{L}_f}{da}=\frac{m_f\times Hr{c}_f\times }{t_f}+\frac{K_{\theta }{}_{,}{}_f}{K_{\theta }{}_{,}{}_f+K_{\theta }{}_{,}{}_r}[\frac{m_f(Hcg-Hr{c}_f)+m_r(Hcg-Hr{c}_r)}{t_f}]$

Load Transfer Distribution

The lateral load transfer distribution is the ratio between the axle's lateral load transfer sensitivity and the total lateral load transfer sensitivity.

$LLT{D}_f=\frac{\frac{d\mathrm{\Delta }TOTA{L}_f}{da}}{\frac{d\mathrm{\Delta }TOTA{L}_f}{da}+\frac{d\mathrm{\Delta }TOTA{L}_r}{da}}$

A LLTD_f of 60% means 60% of the vehicles total vertical tire load due to lateral acceleration is occurring on the front axle.

Traction

Load transfer causes a change in traction in each wheel. The result of one pair of tires being loaded more than the other pair is a net loss in total traction. This can be explained by tire load sensitivity.

The amount of load each tire receives during a given motion can be changed by modifying spring rates or through the use of anti-roll bar. An anti-roll bar does not change the load of the inside tire relative to the outside tire but rather front-to-rear load distribution during lateral acceleration. This is also the case with springs. If you want to ignore all that dumb math it essentially can be broken down into the following:

1. total lateral load cannot be changed with suspension
2. the distribution of lateral load can be changed with suspension by changing roll stiffness and roll centers
3. an increase in rear lateral load means a decrease in front lateral load and vice versa
4. increase in rear lateral load means increase in oversteer bias

Increasing the stiffness of an axle's anti-roll bar or springs will increase the amount of load that axle's outside tire will receive. It will also decrease the amount of load the other axle's outside tire will receive. This is because they are inversely related.

Sources

• Simplified steady-state lateral load transfer analysis for spring rate and anti-roll bar selection | Kelvin Tse
• Geometric & Elastic Weight Transfer and the Roll Centre